Visualisation du comportement des transformateurs : Dessiner des diagrammes de phasors et des circuits équivalents.

Les diagrammes en phaseurs sont des représentations graphiques qui aident à analyser le comportement des grandeurs électriques dans les circuits CA. Lorsqu’ils sont appliqués aux transformateurs, les diagrammes en phaseurs montrent la relation entre le courant, la tension et la puissance dans les conditions de charge et sans charge.

Image used courtesy of Adobe Stock

Les schémas équivalents peuvent être utilisés pour représenter les transformateurs de manière simplifiée. Le schéma équivalent pour une condition sans charge comprend la branche d’aimantation, qui tient compte du courant d’aimantation et des pertes dans le noyau. En état de charge, le schéma équivalent se compose de la branche d’impédance série (comprenant la résistance et la réactance), ce qui représente la chute de tension aux bornes des enroulements du transformateur (primaire et secondaire) et de l’impédance de charge.

Conditions sans Charge du Transformateur

Lorsque les bornes de sortie d’un transformateur ne sont pas connectées, on parle de condition sans charge. Pendant cet état, aucun courant ne circule dans les enroulements secondaires. Cependant, une tension alternative appliquée aux bornes d’entrée induit un faible courant primaire, qui génère le flux magnétique dans le noyau. Ce courant est communément appelé courant d’aimantation. Des pertes d’hystérésis se produisent lorsque le flux magnétique dans un noyau augmente continuellement jusqu’à son niveau de crête dans une direction, s’inverse pour atteindre un pic dans la direction opposée, et que le noyau absorbe de l’énergie. Des courants de Foucault sont également induits dans le noyau du transformateur en raison du flux magnétique alternatif, ce qui entraîne une dissipation d’énergie supplémentaire dans le noyau.

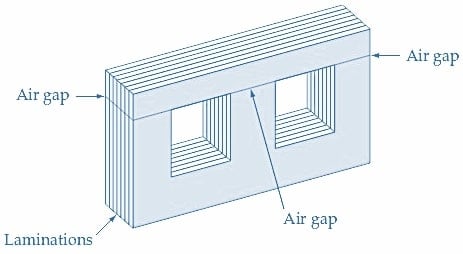
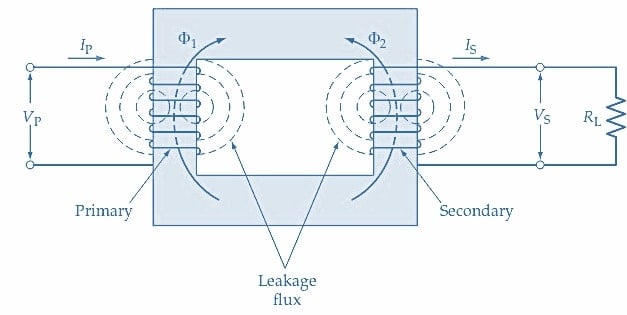
Pour minimiser les pertes d’hystérésis, il est crucial d’utiliser un matériau magnétique avec une boucle d’hystérésis étroite, et le noyau du transformateur est construit sous forme de laminations pour minimiser les pertes par courants de Foucault. Cependant, la construction stratifiée introduit des entrefer dans le noyau, comme le montre la Figure 1, et le courant d’aimantation doit créer un flux à la fois dans le noyau et dans les entrefer. En plus de ces pertes, il y a également une perte I²R dans les enroulements primaires du transformateur qui doit être fournie. Par conséquent, le courant sans charge primaire comprend le courant d’aimantation et le courant nécessaire pour fournir les pertes dans le noyau.

Figure 1. Le noyau d’un transformateur présente des pertes d’énergie dues aux courants de Foucault et aux entrefer. Le courant sans charge primaire doit fournir ces pertes dans le noyau ainsi qu’un flux magnétique dans le noyau. Image utilisée avec l’aimable autorisation de Amna Ahmad

Diagramme en Phaseur sans Charge

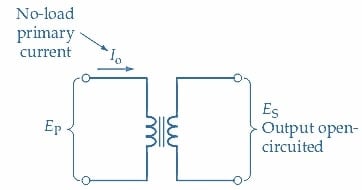
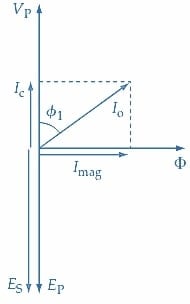
Le circuit du transformateur et un diagramme en phaseur approximatif en condition sans charge sont illustrés à la Figure 2. Comme les enroulements du transformateur sont inductifs, la tension d’entrée V_P devance le courant d’aimantation (I_mag) de 90°.

(a) Circuit d’un transformateur avec sortie ouverte

(b) Diagramme en phaseur approximatif

Figure 2. Circuit et diagramme en phaseur pour un transformateur hors charge. Le flux du noyau (ɸ) est en phase avec le courant d’aimantation (I_mag). Les enroulements sont inductifs, donc I_mag retarde la tension primaire (V_P) de 90°. Image utilisée avec l’aimable autorisation de Amna Ahmad

Le courant d’aimantation entraîne une fluctuation du flux (ɸ), ce qui a pour conséquence que le phasor du flux est en phase avec Imag. I_C est la partie du courant primaire responsable de la fourniture des pertes dans le noyau et d’une perte de puissance mineure dans l’enroulement primaire. La perte totale de puissance est égale à (I_C×V_P), et par conséquent, I_C est en phase avec V_P. Le courant sans charge primaire (I_o) est le résultat de la somme en phaseurs de I_mag et de I_C. Étant donné que I_C est généralement beaucoup plus petit que I_mag, le facteur de puissance à vide (cos ɸ₁) est assez faible. Les tensions induites dans les enroulements secondaire et primaire, E_S et E_P, respectivement, retardent le flux de 90°, de sorte que les phaseurs E_S et E_P sont dessinés en opposition au phaseur V_P. Dans la Figure 2, E_S et E_P sont montrés comme des tensions égales (c.-à-d. en supposant un transformateur 1:1). Une approximation dans le diagramme en phaseur de la Figure 2 se produit parce qu’E_P a été pris comme exactement égal et opposé à V_P. En réalité, E_P est égal et opposé à la somme des phaseurs de V_P, et les chutes de tension de l’enroulement dues à l_o. Cela devient plus évident lorsqu’on considère un transformateur en charge.

Schéma Équivalent sans Charge

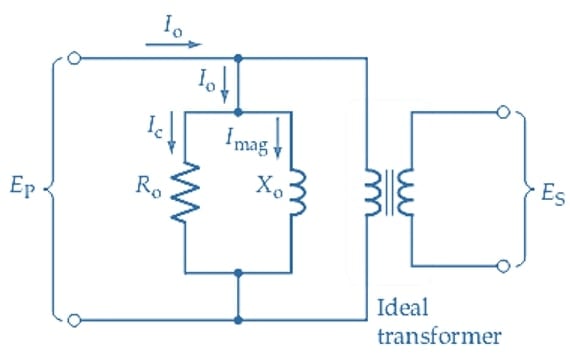
La Figure 3 montre le schéma équivalent du transformateur lorsqu’il est en condition sans charge. Dans ce circuit, un transformateur idéal remplace le transformateur réel, et il a une résistance parallèle R_o et une réactance inductive X_o à son côté primaire. R_o est utilisée pour représenter les pertes dans le noyau, et le courant I_C qui fournit les pertes dans le noyau y circule. X_o représente une bobine sans perte qui porte le courant d’aimantation I_mag. Ainsi, R_a, X_o et le transformateur idéal simulent ensemble l’état sans charge réel du transformateur.

Figure 3. Le schéma équivalent sans charge d’un transformateur est composé d’un transformateur idéal (sans perte) avec son primaire en parallèle avec une résistance (R_o) représentant les pertes dans le noyau et une réactance inductive (X_o) pour représenter l’inductance de l’enroulement. Image utilisée avec l’aimable autorisation de Amna Ahmad

Transformateur en Charge

Lorsqu’une charge est connectée à l’enroulement secondaire d’un transformateur, un courant circule dans le circuit secondaire. Comme illustré à la Figure 4, le courant secondaire a tendance à générer un flux ɸ₂dans le noyau du transformateur. Pour alimenter le courant secondaire, le courant doit circuler dans l’enroulement primaire. Le courant primaire génère un flux ɸ₁qui est exactement égal et opposé à ɸ₂. Ainsi, ɸ₁ et ɸ₂ s’annulent mutuellement, et le flux du noyau reste au niveau établi par le courant d’aimantation.

Sur la Figure 4, il est illustré que lorsque des courants circulent dans les enroulements primaire et secondaire d’un transformateur, tous les flux créés par les courants ne traversent pas le noyau en fer. Une partie du flux passe à travers l’air qui entoure chaque bobine, ce qui est appelé flux de fuite. Étant donné que le chemin magnétique dans le noyau en fer offre beaucoup moins de résistance que le chemin de l’air autour de chaque bobine, la quantité de flux de fuite est généralement faible. Cependant, le flux de fuite se lie encore avec les spires d’enroulement dans chaque bobine, ce qui entraîne la génération de FEM qui s’opposent au courant qui traverse chaque bobine. Cela est similaire à une inductance indésirable connectée en série avec chaque enroulement, qui est appelée inductance de fuite.

Figure 4. Les courants circulant dans les enroulements primaire et secondaire d’un transformateur génèrent des flux de noyau (ɸ₁ et ɸ₂). Il se produit également un flux de fuite autour de chaque enroulement. Image utilisée avec l’aimable autorisation de Amna Ahmad

Schéma Équivalent Complet

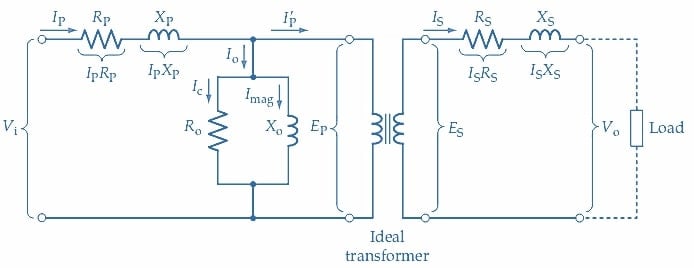
La Figure 5 montre le schéma équivalent complet d’un transformateur. Celui-ci comprend les inductances de fuite des enroulements primaire et secondaire, représentées par les réactances inductives X_P et X_S, respectivement, ainsi que les résistances d’enroulement R_P et R_S. R_S et X_S sont connectées en série avec l’enroulement secondaire, ce qui provoque une chute de tension lorsque le courant de charge est présent. De même, R_P et X_P sont connectées en série avec l’enroulement primaire, ce qui entraîne des chutes de tension lorsque circule un courant primaire. R_o et X_o restent en parallèle avec le primaire pour imiter les pertes sans charge et le courant d’aimantation du transformateur, respectivement.

Figure 5. Le schéma équivalent complet d’un transformateur est simplement le schéma équivalent sans charge (Figure 3) avec les composants R_P, X_P, R_S et X_S  inclus pour représenter les résistances d’enroulement et les inductances de fuite. Image utilisée avec l’aimable autorisation de Amna Ahmad

Diagramme en Phaseur pour le Circuit Secondaire

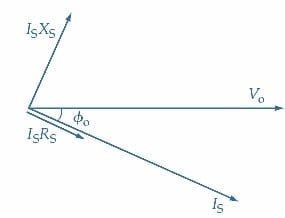
Le diagramme en phaseur pour le circuit secondaire d’un transformateur en charge est présenté à la Figure 6. En se référant aux Figures 5 et 6(a), Vo est la tension aux bornes de sortie du transformateur, et IS est le courant secondaire (de charge). Pour une charge avec un angle de décalage (ɸ_O) en retard, le phasor I_S est représenté en retard par rapport au phasor V_o par un angle de ɸ_o. Le courant secondaire circule à travers R_S et X_S et produit des chutes de tension : I_SR_S et I_SX_S. La chute de tension résistive (ISRS) est en phase avec IS, et la chute de tension inductive (ISXS) précède le courant de 90°, comme illustré à la Figure 6(a).

(a) Diagramme en phaseur partiel pour un circuit secondaire avec une charge inductive (décalage ɸ)

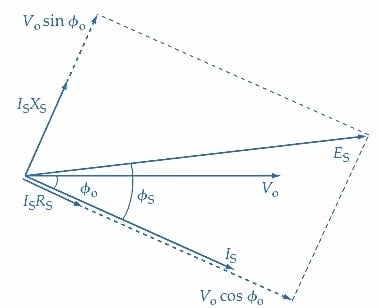
(b) E_S est la somme en phaseurs de V_o, I_SX_S et I_SR_S

Figure 6. Diagramme en phaseur pour le circuit secondaire d’un transformateur en charge. Le courant secondaire I_S retarde la tension de sortie Vo de l’angle de charge ɸo. Les tensions (I_SX_S) et (I_SR_S) sont les chutes de tension aux bornes de X_S et R_S. La tension induite au secondaire E_S est la somme en phaseurs de Vo, (I_SX_S) et (I_SR_S). Image utilisée avec l’aimable autorisation de Amna Ahmad

Sur la Figure 6(b), les phaseurs de V_O, I_S, I_SX_S et I_SR_S sont reproduits à partir de la Figure 6(a). La tension induite au secondaire E_S (voir aussi la Figure 5) est la somme en phaseurs de V_o, I_SR_S et I_SX_S.

\[E_{S}=\sqrt{(V_{O}\,cos\,cos\,\Phi_{O}+I_{S}R_{S})^{2}+(V_{O}\,sin\,sin\,\Phi_{O}+I_{S}X_{S})^{2}}(1)\]

et l’angle de phase entre E_S et I_S est

\[\Phi_{S}=\Big( \frac{V_{O}sinsin\Phi_{O}+I_{S}X_{S}}{V_{O}+I_{S}X_{S}}\Big)(2)\]

Étant donné que la tension induite au secondaire retarde toujours de 90° par rapport au flux du noyau ɸ, le phasor du flux du noyau peut être dessiné avec un retard de 90° par rapport à E_S.

Diagramme en Phaseur pour le Primaire

Le diagramme en phaseur pour le primaire d’un transformateur peut être construit de manière similaire à celui qui vient d’être discuté pour le secondaire. Dans ce cas, il est nécessaire de commencer par la tension E_P et le courant I_P directement à l’enroulement primaire (voir Figure 5). E_P et I_P‘ peuvent être calculés à partir de la connaissance du rapport de transformation, du courant et de la tension secondaire. L’angle de phase entre E_P et I_P‘ est ɸ_S, l’angle de phase du circuit secondaire.

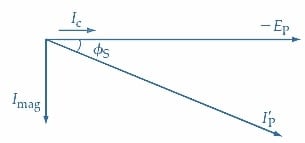
En se référant à la Figure 7(a), le phasor -E_P est d’abord dessiné horizontalement, et le phasor du courant IP’ est dessiné avec un angle de retard de ɸ_S par rapport à -E_P. Remarquez que, puisque E_P est la tension induite dans l’enroulement primaire par le flux magnétique changeant, elle est égale et opposée à la composante de la tension appliquée à l’enroulement primaire (idéal). En conséquence, la composante de tension appliquée est -E_P.

(a) IP’ retarde -E_P de ɸ_S

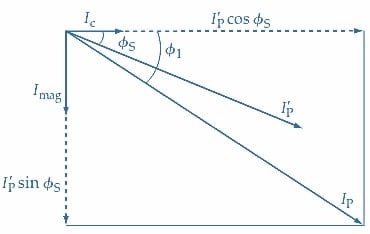
(b) I_P est la somme en phaseurs IP’, I_mag et I_C

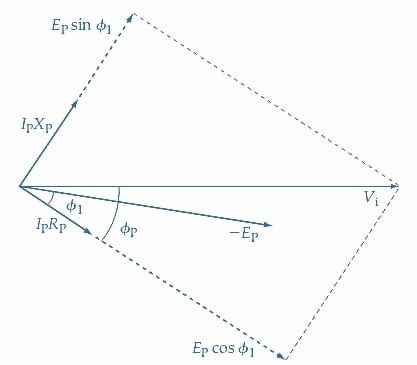
(c) V_i est la somme en phaseurs -E_P, I_PX_P et I_PR_P

Figure 7. Diagramme en phaseur pour le primaire d’un transformateur sous charge. Le courant primaire (IP’) retarde la tension primaire (E_P) de l’angle de phase du secondaire (ɸ_S). Les courants sans charge I_C et I_mag sont également inclus, et le courant primaire total (I_P) est la somme en phaseurs de IP’, I_C, et I_mag. La tension d’alimentation (V_i) est la somme en phaseurs de -E_P, (I_PX_P), et (I_PR_P). Image utilisée avec l’aimable autorisation de Amna Ahmad

En plus de IP’, le courant sans charge I_o (composé de I_C et I_mag) doit être fourni. Le courant réel prélevé sur l’alimentation est I_P, qui est la somme en phaseurs de IP’, I_C et I_mag comme le montrent les Figures 5 et 7(b).

\[I_{P}\sqrt{(I^{‘}_{P}\,cos\,cos\,\Phi_{S}+I_{C})^{2}}+(I^{‘}_{P}+I_{mag})^{2}(3)\]

Et

\[\Phi_{1}=\Big(\frac{I^{‘}_{P}sin\,sin\,\Phi_{S}+I_{mag}}{I^{‘}_{P}+I_{C}}\Big)(4)\]

Le courant primaire (I_P) produit une chute de tension le long de R_P et X_P (Figure 5). Le phasor I_PR_P est en phase avec I_P, et le phasor I_PX_P précède I_P de 90°, comme illustré à la Figure 7(c). La somme en phaseurs de I_PR_P, I_PX_P et -E_P donne la tension d’alimentation V_i. Comme illustré, l’angle de phase d’entrée primaire est ɸ_P, l’angle entre V_i et I_P

Étant donné la charge secondaire et les paramètres du schéma équivalent du transformateur, la tension et le courant d’entrée primaire peuvent être calculés à l’aide du diagramme en phaseur.

Points à retenir des Diagrammes en Phaseur et Schémas Équivalents pour les Transformateurs

Le diagramme en phaseur et le schéma équivalent d’un transformateur apportent des informations précieuses sur le comportement électrique du transformateur dans les conditions de charge et sans charge. Ces concepts permettent d’analyser la régulation de tension, les pertes de puissance et l’efficacité du transformateur. Par conséquent, il est crucial de comprendre parfaitement le diagramme en phaseur et le schéma équivalent afin de garantir un fonctionnement sûr et efficace des transformateurs.